Reinforcement Learning from Human Feedback (RLHF): Aligning LLMs with Human Intent

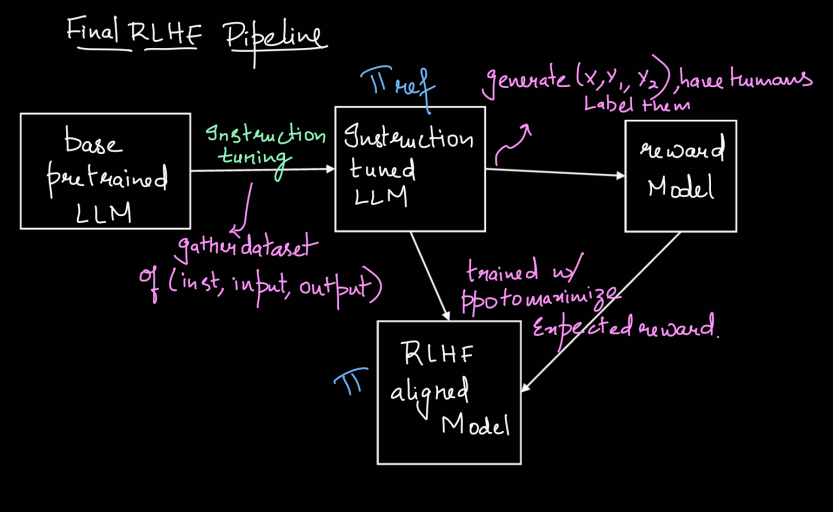
Reinforcement Learning from Human Feedback (RLHF) is a pivotal technique in the advancement of large language models (LLMs), aiming to align their behavior more closely with human intentions and ethical standards. While starting with a large pretrained LLM—such as LLaMA 2 with its 7 billion parameters trained on a trillion tokens—provides a strong foundation, these models can still struggle with handling harmful or toxic queries effectively. To address these challenges, RLHF builds upon initial steps of alignment, beginning with instruction tuning (Supervised Fine-Tuning or SFT).

Instruction tuning involves fine-tuning the pretrained model using curated instruction-response pairs, enabling the model to follow specific directives more accurately. However, to further refine the model’s ability to adhere to human values and preferences, RLHF incorporates a feedback loop where human evaluators assess the model’s outputs. This feedback is then used to guide the model in generating responses that not only follow instructions but also align with desired ethical and practical outcomes. By integrating RLHF, developers can enhance the model’s reliability, ensuring it behaves appropriately across a wide range of scenarios, including those involving sensitive or complex queries.

Limitations of Instruction Tuning

Instruction tuning has been instrumental in enhancing language models by aligning their responses with specific tasks and desired behaviors. However, it possesses several key limitations that can affect the model’s performance and reliability.

1. No Learning from Negative Feedback

Instruction tuning relies solely on positive examples, aiming to maximize the likelihood of correct responses. If a model generates an incorrect or suboptimal answer, it doesn’t receive any corrective feedback. This lack of negative reinforcement means the model may repeat mistakes without understanding what went wrong.

2. Limited Diversity in Acceptable Outputs

Many prompts, particularly creative ones, have multiple valid responses. However, instruction tuning typically provides only one example per instruction, restricting the model’s ability to produce varied and imaginative outputs. This can lead to repetitive and less engaging responses that closely mirror the training examples.

3. Difficulty in Abstaining When Uncertain

Models fine-tuned through instruction tuning often struggle to recognize when they lack sufficient information to provide an accurate answer. Instead of admitting uncertainty, they may generate plausible-sounding but incorrect responses, known as hallucinations. This is especially problematic for knowledge-based tasks where accuracy is crucial.

4. Exclusion of Human Preferences

Instruction tuning does not incorporate nuanced human preferences or judgments. While it can guide models to follow specific instructions, it lacks the mechanism to evaluate and prioritize responses based on what users find most valuable or enjoyable. Consequently, models may produce technically correct answers that do not fully align with user expectations.

5. Challenges with Task Diversity and Consistency

Balancing a wide range of tasks—from creative writing to factual reporting—within a single instruction tuning framework can lead to inconsistencies. Creative tasks encourage imaginative content, while factual tasks demand accuracy. This duality can cause models to apply inappropriate generation strategies, resulting in unreliable answers for certain prompts.

6. Theoretical Limitations: Absence of Interactive Learning

From a theoretical standpoint, supervised instruction tuning only provides positive feedback, limiting the model’s ability to correct incorrect hypotheses. Without the opportunity to receive negative feedback, models are more susceptible to adopting flawed patterns if the training data is incomplete or biased. RLHF mitigates this by allowing models to generate their own responses and receive comprehensive feedback, enhancing their ability to generalize correctly.

7. Inability to Effectively Teach Abstention

Training models to recognize when they do not know an answer and to abstain from responding is challenging with instruction tuning. Without clear indicators of uncertainty, models cannot reliably determine when to say “I don’t know.” While partial solutions exist, such as prompting models to abstain for specific questions, achieving genuine uncertainty-based abstention remains an open research area.

8. Implications for Model Stealing and Distillation

When smaller models are trained to replicate the behavior of larger, proprietary models using supervised learning alone, they may inherit the same limitations, such as fabricating answers for knowledge-seeking queries. Without RLHF, these distilled models struggle to maintain factual accuracy and reliability, highlighting the necessity of incorporating reinforcement learning techniques.

Conclusion

While instruction tuning effectively guides language models through positive examples and specific instructions, its limitations—including the inability to learn from negative feedback, restricted output diversity, challenges in recognizing uncertainty, exclusion of human preferences, and inconsistencies across diverse tasks—underscore the need for more advanced training methodologies. Reinforcement Learning from Human Feedback (RLHF) addresses these shortcomings by incorporating both positive and negative feedback, enabling models to produce more truthful, reliable, and diverse responses. By leveraging RLHF, developers can create language models that better align with human preferences and factual accuracy, overcoming the inherent limitations of instruction tuning alone.

Question:

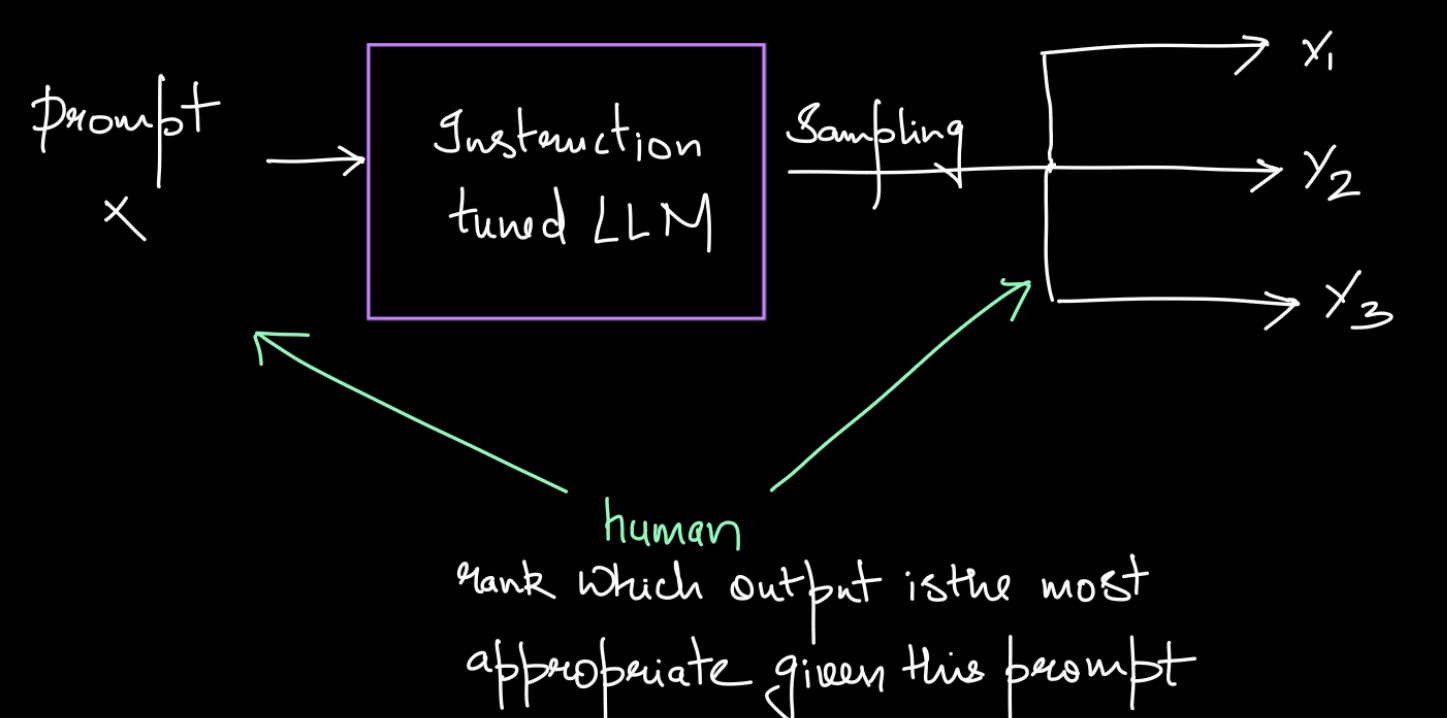
“How do we incorporate human preference to address the above issues?”

Comparison of 32-bit, 16-bit, and bfloat16 floating-point formats.

Comparison of 32-bit, 16-bit, and bfloat16 floating-point formats. (Maxime Labonne)

Limitations: Extremely Expensive to Collect

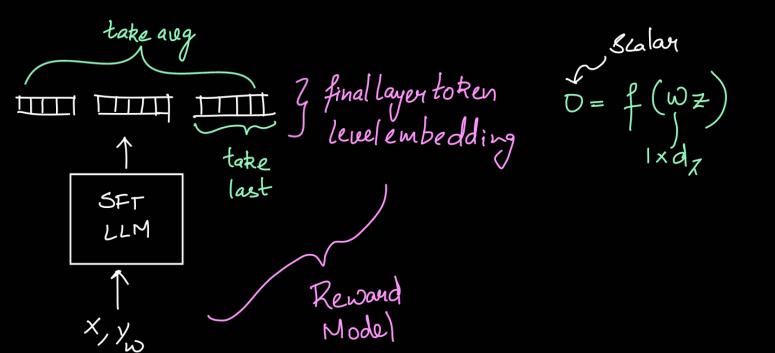
Reward Model
Idea: Can we train a model to predict human preference judgment?

  • Input: prompt $ x $, Output $ y_i $
  • Output: Scalar score

Starting with the Bradley-Terry model for pairwise preference:

$$ P(y_0 > y_1 | x) = \frac{\exp(r(x, y_0))}{\exp(r(x, y_0)) + \exp(r(x, y_1))} $$

Where:

  • $ P(y_0 > y_1 | x) $ is the probability that $ y_0 $ is preferred over $ y_1 $ given prompt $ x $.
  • $ r(x, y_0) $ and $ r(x, y_1) $ are the reward (or scalar value) for outputs $ y_0 $ and $ y_1 $ respectively, given the prompt $ x $.

Next, we define the loss function for training the reward model, which aims to maximize the probability of the preferred output $ y_0 $. The loss function is derived from the negative log-likelihood of the Bradley-Terry probability:

$$ L = -\log \left( P(y_0 > y_1 | x) \right) $$

Substituting the Bradley-Terry expression for the probability:

$$ L = -\log \left( \frac{\exp(r(x, y_0))}{\exp(r(x, y_0)) + \exp(r(x, y_1))} \right) $$

This simplifies to:

$$ L = -\log \left( \frac{1}{1 + \exp(r(x, y_1) - r(x, y_0))} \right) $$

Using the definition of the logistic (sigmoid) function $ \sigma(z) = \frac{1}{1 + \exp(-z)} $, we get:

$$ L = -\log \left( \sigma(r(x, y_0) - r(x, y_1)) \right) $$

Thus, the loss function becomes:

$$ L = -\log \sigma \left( r(x, y_0) - r(x, y_1) \right) $$

This loss function is minimized when the model correctly predicts that $ y_0 $ (the preferred output) has a higher reward than $ y_1 $ (the less preferred output), effectively training the model to align with human preferences.

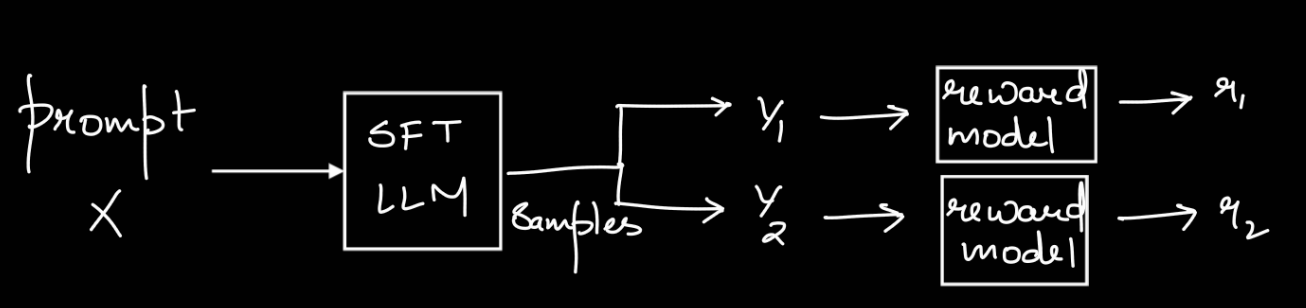
The reward model can be

Comparison of 32-bit, 16-bit, and bfloat16 floating-point formats.

Comparison of 32-bit, 16-bit, and bfloat16 floating-point formats. (Maxime Labonne)

using the reward model.

Comparison of 32-bit, 16-bit, and bfloat16 floating-point formats.

Comparison of 32-bit, 16-bit, and bfloat16 floating-point formats. (Maxime Labonne)

Transcript:

How do we use this to align LLMs to human preferences?

  1. “Best-of-n” Sampling (Rejection Sampling):
    • Generate $ n $ samples for a given prompt, score each with the reward model, and choose the sample with the highest reward.
    • Limitations: Very slow & expensive computationally.
  1. Another approach would be to further fine-tune the SFT LLM (instead of having a separate reward model):
    • Just fine-tune the LLM to maximize $ P(y_0 | x) $.
    • $\rightarrow$ RAFT
    • Issue: The model doesn’t see the n samples.
  1. Use reinforcement learning to increase $ P(y_0 | x) $ by a small amount & decrease $ P(y_1 | x) $ by a small amount, where amounts are functions of $ R(x, y_0) $` and $ R(x, y_1) $.

RLHF:

  • Observe a reward only after generating a complete sequence.

Transcript:

PPO
Read on own

Let me take a stab at explanining the concepts of Policy optimization (PPO is a type of Policy optimization problem)

$\pi_{\text{ref}} \Rightarrow \text{SFT LLM Checkpoint}$
$\pi \Rightarrow \text{Current policy model}$
$\Rightarrow \text{init } \pi = \pi_{\text{ref}}$

$$ \max_{\pi} \mathbb{E}_{x, y} [ r(x, y) - \beta D_{\text{KL}} \left( \pi(y | x) | \pi_{\text{ref}}(y | x) \right) ] $$

  • Reward $ r(x, y) $
  • KL penalty to prevent huge deviations from $\pi_{\text{ref}}$

$$ D_{\text{KL}} \left( \pi(y | x) | \pi_{\text{ref}}(y | x) \right) = \log \frac{\pi(w_i | w_{0, \dots, i-1}, x)}{\pi_{\text{ref}}(w_i | w_{0, \dots, i-1}, x)} $$

  • Optimize using PPO algorithm (e.g., ChatGPT, GPT-4)
  • Can also use REINFORCE (e.g., Gemini)
Comparison of 32-bit, 16-bit, and bfloat16 floating-point formats.

Comparison of 32-bit, 16-bit, and bfloat16 floating-point formats. (Maxime Labonne)